| Este artigo é patrocinado por: «A sua instituição aqui» |
Significado de Disjunção
No âmbito da lógica, uma disjunção é uma proposição da forma “P ou Q” em que P e Q são as disjuntas, isto é, as proposições que formam a disjunção. Assim apresentada, toda a disjunção é uma disjunção inclusiva, o que significa que a mesma só é falsa se ambas as disjuntas forem falsas. Opõe-se, portanto à disjunção exclusiva (da forma “ou P ou Q”) a qual só é verdadeira se as disjuntas tiverem valores de verdade diferentes.
Na matemática é geralmente usado o símbolo ‘∨‘ para indicar uma disjunção. Outros símbolos utilizados em vários contextos são a barra vertical ‘|‘, duas barras verticais ‘||‘, o símbolo da soma ‘+‘, ou a palavra ‘OR‘.
Na lógica binária, em que ocorrem apenas dois estados: Verdadeiro (V) ou Falso (F), a tabela da verdade para uma disjunção com as acontecimentos ‘a’ e ‘b’, é a seguinte:
| a | b | a∨b |
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
Tal significa que basta que um dos acontecimentos seja verdadeiro, para que a disjunção sejam também seja verdadeira. Dito de outra forma, é necessário que todos os acontecimentos sejam falsos para que a disjunção também seja falsa.
O conceito de disjunção também é muito utilizado na análise de conjuntos. Uma disjunção de dois conjuntos, é formada por todos os elementos que constituem os dois conjuntos, quer esses elementos pertençam a ambos os conjuntos ou apenas a um deles. Nos seguintes diagramas de Venn, a disjunção é toda a região de cor vermelha.
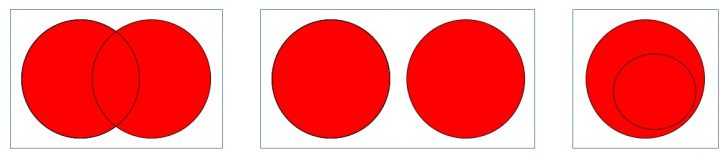
Propriedade da disjunção
A disjunção apresenta várias propriedades, sendo as mais importantes as seguintes:
- Comutatividade: a ∨ b ≡ b ∨ a
- Associatividade: ( a ∨ b ) ∨ c ≡ a ∨ ( b ∨ c ) ≡ a ∨ b ∨ c
- Universalidade: a ∨ ¬ a ≡ 1
- Falsidade é o elemento neutro da disjunção: a ∨ 0 ≡ a
- Verdade é o elemento absorvente da disjunção: a ∨ 1 ≡ 1
- Leis de De Morgan: a ∨ b ≡ ¬ ( ¬ a ∧ ¬ b )



