A Astroide é um tipo específico de hipocicloide, apresentando-se como uma curva com quatro vértices, dada por um ponto num círculo, deslizando ao longo do interior de um círculo maior. Para que se forme a astroide o diâmetro do círculo maior é exatamente quatro vezes maior do que o diâmetro do círculo menor.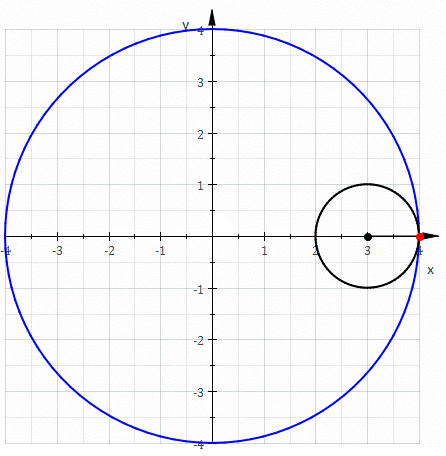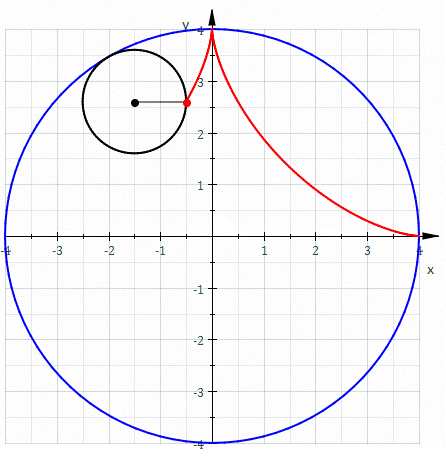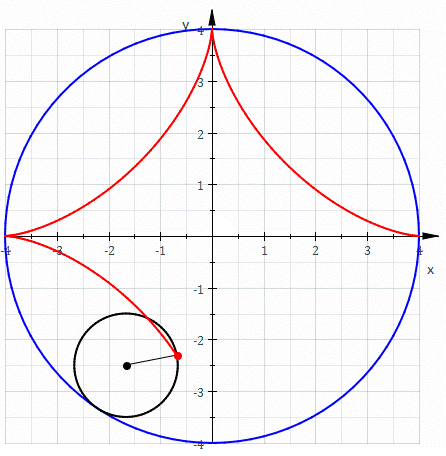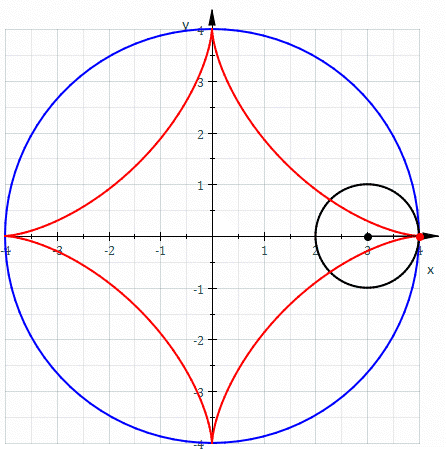
Devido às suas intrigantes propriedades, a astroide foi estudada desde há séculos por diversos matemáticos. Quem se debruçou pela primeira vez sobre esta curva foi o matemático e astrónomo dinamarquês, Ole Cristensen Romer (1644-1710), em resultado da sua procura por dentados com formas mais úteis. Mais tarde, matemáticos célebres como Johann Bernoulli, Gottfried Leibniz ou Jean d’Alembert se deixaram fascinar pela Astroide.
A equação da astroide é a seguinte: x(2/3) + y(2/3) = R(2/3), em que R é o raio do círculo fixo maior e R/4 é o raio do círculo menor que gira no seu interior. O seu comprimento é 6R e a área é 3πR2/8. Um curiosidade é o facto do seu comprimento não depender de π apesar de ser gerada a partir do movimento de dois círculos. Em 1725 Bernoulli que uma astroide é também delineada pela mesma curva que tem 3/4 do diâmetro do círculo fixo maior, ou seja, este delineia a mesma curva do círculo interior apenas com 1/4 do diâmetro do maior. Outra curiosidade é o facto das linhas tangentes ao longa da astroide terem, no seu conjunto, o mesmo comprimento quando prolongadas até tocarem os eixos x e y.
Existe uma petente norte-americana (Patente US 4.987.984) que descreve o uso de uma astroide para embraiagens mecânicas: “a astroide fornece a mesma dispersão de tensão adequada daquela que o arco circular equivalente forneceria, embora retire menos aceleração da came, conferindo uma estrutura mais forte”.




