Un Rectángulo Áureo (o rectángulo dorado, o rectángulo de oro) es un rectángulo cuyos lados a y b están en la proporción áurea, es decir a/b=Φ=1.61803…
Un Rectángulo Áureo (o rectángulo dorado, o rectángulo de oro) es un rectángulo cuyos lados a y b están en la proporción áurea, es decir a/b=Φ=1.61803… Esto significa que el lado menor (b) es el segmento áureo del lado mayor (a).

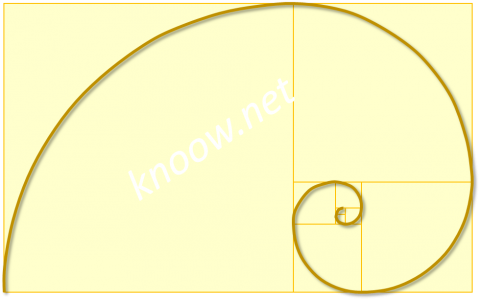
Es interesante el hecho de que es posible dividir este rectángulo en un cuadrado y en otro rectángulo de menor dimensión, siendo que este rectángulo es también un rectángulo áureo. Repitiendo este proceso indefinidamente, se obtiene la siguiente figura:

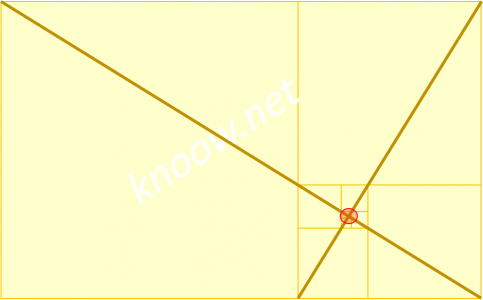
Si dibujamos una diagonal desde el lado superior izquierdo al lado inferior derecho del rectángulo mayor y otra desde el lado superior derecho al lado inferior izquierdo del segundo rectángulo mayor, el punto de intersección muestra el punto para donde todos los rectángulos convergen. Por otro lado, las longitudes de las diagonales se encuentran en la proporción áurea de cada uno. Al punto en el que todos convergen se le llama ‘Ojo de Dios’.
Si unimos los vértices del diagrama, obtenemos una espiral logarítmica que ‘envuelve’ el ‘Ojo de Dios’. Estas espirales se encuentran con gran frecuencia en la naturaleza: en las conchas, en los cuernos de los animales, en la cóclea del oído. Esto sucede porque la naturaleza siente la necesidad de rellenar el espacio durante la fase de crecimiento de forma económica y regular – esta espiral, además de fuerte, minimiza la cantidad de materiales necesarios y a medida que se expande, su dimensión se altera pero su forma se mantiene inalterada.