Um Retângulo Áureo (ou retângulo dourado, ou ainda retângulo de ouro) é um retângulo cujos lados a e b estão na proporção áurea, isto é a/b=Φ=1.61803… Tal significa que o lado menor (b) é o segmento áureo do lado maior (a).
Interessante é o facto de que é possível dividir este retângulo num quadrado e num outro retângulo de menor dimensão, sendo que este retângulo é também um retângulo áureo. Repetindo este processo indefinidamente, obtém-se a seguinte figura:
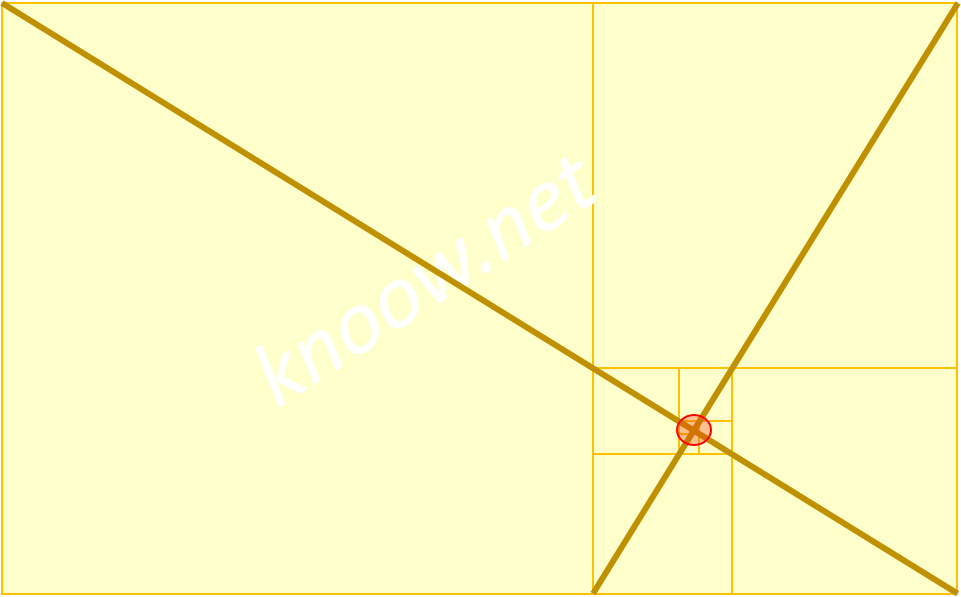
Se desenharmos uma diagnonal do lado superior esquerdo ao lado inferior direito do retângulo maior e uma outra do lado superior direito ao lado inferior esquerdo do segundo retângulo maior, o ponto de interseção mostra o ponto para onde todos os retângulos convergem. Por outro lado, os comprimentos das diagonais encontram-se na proporção áurea de cada um. Ao ponto para o qual todos dos retângulo convergem é dado o nome de ‘Olho de Deus’.
Se ligarmos os vértices do diagrama, obtemos uma espiral logarítmica que ‘envolve’ o ‘Olho de Deus’. Estas espirais são encontradas com grande frequência na natureza: nas conchas, nos chifres dos animais, na cóclea do ouvido. Tal acontece porque a natureza sente necessidade de preencher o espaço durante a fase de crescimento de forma económica e regular – esta espiral, além de forte, minimiza a quantidade de materiais necessários e à medida que se expande, a sua dimensão altera-se mas a sua forma mantém-se inalterada.