O que é o Triângulo de Reuleaux
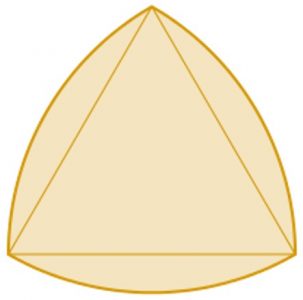O Triângulo de Reuleaux (ou Triângulo Esférico) é um dos polígonos estudados pelo cientista e engenheiro alemão Franz Reuleaux. A característica fundamental deste triângulo (e dos restantes polígonos de Reuleaux) é o facto de serem curvas de largura constante, isto é, a distância entre as duas retas tangentes paralelas opostas é a mesma, qualquer que seja a direção das referidas retas – tal faz com que, ao rodar o triângulo no interior de um quadrado tangente, há sempre quatro pontos de contacto com o quadrado, uma em cada lado.
Após os trabalhos de Reuleaux, e sobretudo após a sua apresentação em 1875, o triângulo passou a ter inúmeras aplicações práticas em diversas áreas da engenharia, principalmente em mecanismos e máquinas, tendo dado origem a numerosas patentes tecnológicas. Um dos exemplos de aplicação prática é em ferramentas de perfuração giratória (brocas) pois permite a execução de furos quadrados. Além das brocas, outras aplicações práticas são garrafas de formato inovador, cilindros, embalagens para líquidos, prateleiras giratórias, caixas de velocidades, motores giratórios, entre muitas outras.
Propriedade do Trângulo de Reuleaux
Além de Reuleaux, muitos outros matemáticos estudaram este triângulo, pelo que atualmente são conhecidas muitas das suas propriedades. Por exemplo, a sua área é A = 1/2 (π – √3) r2 ≈ 0,70477 r2, e a área perfurada é de 0,9877003907(…) da área do quadrado real (a pequena diferença acontece porque a ferramenta de furação produz um quadra com os cantos redondos muito ligeiros. A área de um círculo de igual diâmetro é A = (π/4) r2 ≈ 0,70477 r2.
Como construir o Triângulo de Reuleaux
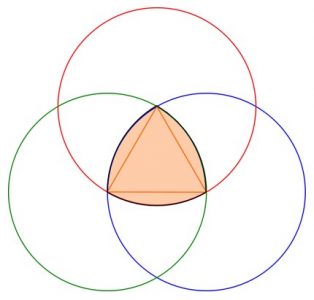
O Triângulo de Reuleaux pode ser construído a partir de três círculos ou, alternativamente a partir do arredondamento dos lados de um triângulo equilátero. A partir um círculo inicial, é desenhado um outro com centro no lado do círculo inicial e com o mesmo diâmetro. Por fim desenha-se um terceiro círculo, com o mesmo diâmetro dos anteriores, e com centro num dos pontos de intercepção dos dois primeiros. A região central deste conjunto é o Triângulo de Reuleaux.
A forma alternativa de construção do Triângulo de Reuleaux é, a partir de um triângulo equilatero, desenhar três arcos em que o centro de cada um é um dos vértices do triângulo e os limites são os outros dois vértices.
